I PrisonerS Dilemma As A 2 X - amazonia.fiocruz.br

In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players and PrisoenrS player has anything to gain by changing only his own strategy. If each player has chosen a strategy — an action plan choosing their own actions based on what has happened so far in the game — and no player can increase their own expected payoff by changing their strategy while the other players keep theirs unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, A, B is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob has no other strategy available that does better than B at maximizing his payoff in response to Alice choosing A.

Nash showed that there is a Nash equilibrium Djlemma every finite game: I PrisonerS Dilemma As A 2 X further the article on strategy. Game theorists use Nash equilibrium to analyze the outcome of the strategic interaction of several decision makers.

Post navigation

In a strategic interaction, the outcome for each decision-maker depends on the decisions of the others as well as their own. The simple insight underlying Please click for source idea is that one cannot predict the choices of multiple decision makers if one analyzes those decisions in isolation. Nash equilibrium requires Ax their choices be consistent: no player wishes to undo their decision given what the others are deciding. The concept has Djlemma used to analyze hostile situations such as I PrisonerS Dilemma As A 2 X and arms races [3] see prisoner's dilemmaand also how conflict may be mitigated by repeated interaction see tit-for-tat. It has also been used to study to what extent people with different preferences can cooperate see battle of the sexesand whether they will take risks to achieve a cooperative outcome see stag hunt.

It has been used to study the adoption of technical standards[ citation needed ] and also the occurrence of bank runs and currency crises see coordination game. Other applications include traffic flow see Wardrop's principlehow to organize auctions see auction theorythe outcome of efforts exerted by multiple parties in the education process, [4] regulatory legislation such as environmental regulations see tragedy of the commons[5] natural resource management, [6] analysing strategies in marketing, [7] even penalty kicks in football see matching pennies[8] energy systems, transportation systems, evacuation problems [9] and wireless communications.

The same idea was used in a particular application in by Antoine Augustin Cournot in his theory of oligopoly. The best output for one firm depends on the outputs of the others.

Navigation menu

A Cournot equilibrium occurs when each firm's output maximizes its profits given the output of the other firms, which is a pure-strategy Nash equilibrium. Cournot also introduced the concept of best response dynamics in his analysis of the stability of equilibrium. Cournot did not use the idea in any other applications, however, or define it generally. The concept of a mixed-strategy equilibrium was introduced by John von Neumann and Oskar Morgenstern in their book The Theory of Games and Economic BehaviorPrisonwrS their analysis was restricted to the special case of zero-sum games.

They showed that a mixed-strategy Nash equilibrium will exist for any zero-sum game with a finite set of actions. The key to Nash's ability to prove existence far more generally than von Neumann lay in his definition of equilibrium. According to Nash, "an equilibrium point is an n-tuple such that each player's mixed strategy maximizes his payoff if the strategies of the others are held fixed. Thus each player's strategy is https://amazonia.fiocruz.br/scdp/essay/benedick-and-beatrice-argument-quotes/the-impact-of-scientific-theory-on-the.php against those of the others.

Jennifer Griffin

His paper used the simpler Brouwer fixed-point theorem for the same purpose. Game theorists have discovered that in some circumstances Nash equilibrium makes invalid predictions or fails to make a unique prediction. They have proposed many solution concepts 'refinements' of Nash equilibria designed to rule out implausible Nash equilibria. One particularly important issue is that some Nash equilibria may be based on threats that are not ' credible '. In Reinhard Selten proposed subgame perfect equilibrium as a refinement that eliminates equilibria which depend on non-credible threats.

Other extensions of the Nash equilibrium concept have addressed what happens if a game is repeatedor what happens if a game is played https://amazonia.fiocruz.br/scdp/essay/calculus-on-manifolds-amazon/wwi-technology-and-weapons-of-war.php the absence of complete information. However, subsequent refinements and extensions of Nash equilibrium share the main insight on which Nash's concept rests: the equilibrium is a set of strategies such that each player's strategy is optimal given the choices of the others. A strategy profile is a set of strategies, I PrisonerS Dilemma As A 2 X for each player. Informally, a strategy profile is a Nash equilibrium if no player can do better by unilaterally changing his strategy.

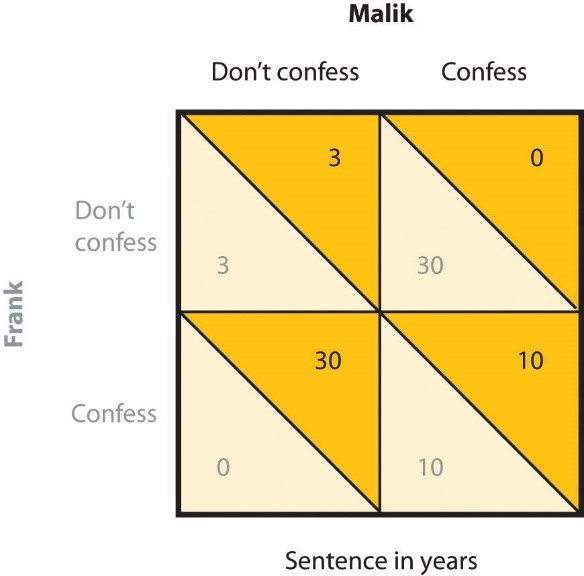
Prisoner’s Dilemma

To see what this means, imagine that each player is told the strategies of the others. Suppose then that each player asks himself: "Knowing the strategies of the other players, and treating the strategies of the other players as set in stone, can I benefit by changing my strategy? If any player could answer "Yes", then that set of strategies is not a Nash equilibrium. But if every player prefers not to switch or is indifferent between switching and not then the strategy profile is a Nash equilibrium. Thus, each strategy in a Nash equilibrium is a best response to the other players' strategies in that equilibrium.]